“Portal-Bouncing” and Oscillations

Scott H. Hawley, Ph.D.

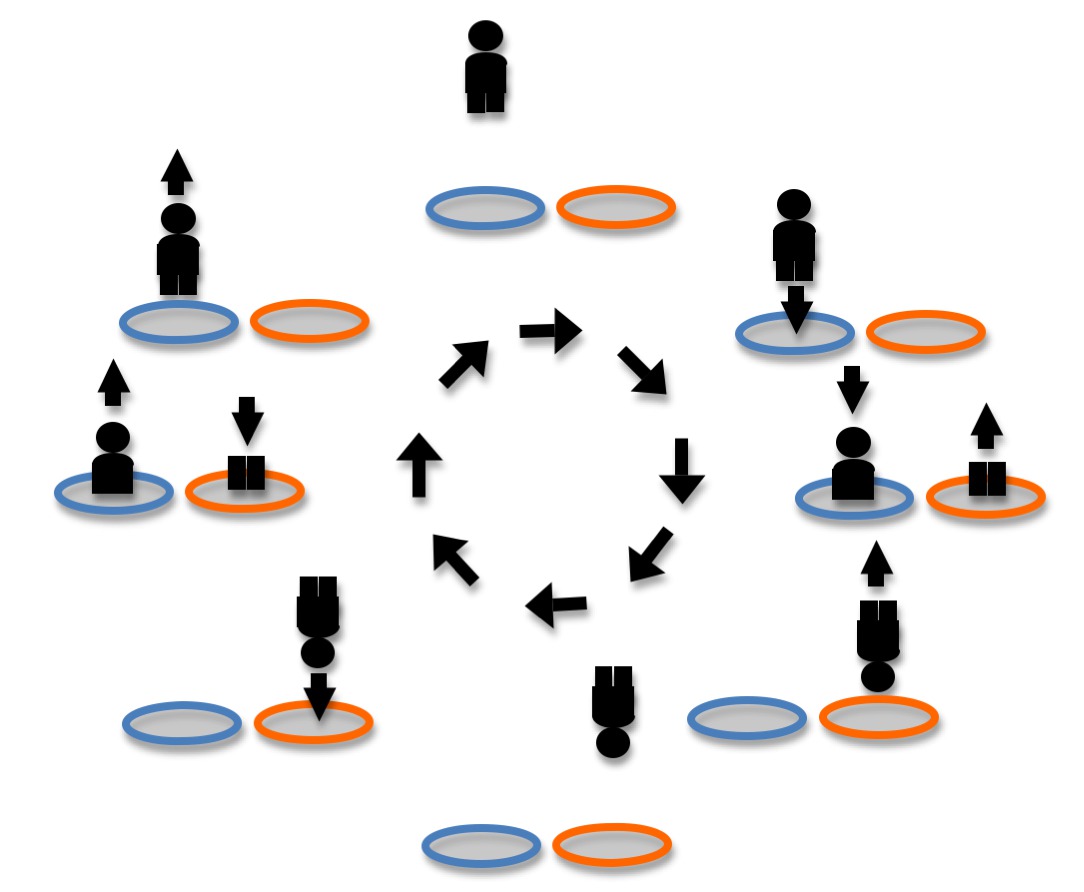
Elementary School:

Open two portals, next to one another, on the floor. Then drop a storage cube – or yourself – inside one of them! See what happens? Whatever gets dropped in one portal, comes out moving upward in the other portal. Then the object – or you – reaches a maximum height, and starts falling, and eventually comes back upward from the original portal! This process repeats itself over and over.

When something moves repeatedly back and forth (or up and down), we say that it is oscillating. Many things in nature oscillate. Can you think of any others?

One example is a pendulum, such as a girl on a swing, going back and forth. In this case, the girl is oscillating. Oscillation is one of the most basic processes in the universe. From piano strings, to tree branches in the wind, even to stars within galaxies, so many things in nature oscillate!

Imagine a little red ball that can roll along a hill. If you start the ball in the place shown, it will roll down and to the right, into the valley and back up on the other side until it comes to a stop.

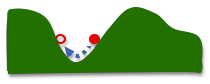
Then it will start rolling back down and to the left, into the valley and up the other side. If there’s not much in the way to slow the ball down, this oscillation will continue for a very long time.

The time it takes for the ball to make it back to its original position is called the period of the oscillation, and it stays the same throughout the motion. Many things in nature have some period of their motion that we use to time things. The time it takes for the moon to go around the earth and come back to its starting point, for example, is called a month. If you or your parents have a digital watch, there’s a tiny crystal inside, and the crystal oscillated with a certain period that is used to tell the time!

Exercise: Now go back to the Portal game. Using a clock or a stopwatch, can you find the period of the box’s (or your) oscillation? Make sure it stays the same as you keep watching the motion!

High School Physics:

The most common type of oscillation you’re likely to study is called Simple Harmonic Motion (SHM) or Simple Harmonic Oscillations (SHO), or more generally, Small Oscillations. For just about every system in nature that oscillates, oscillations with small enough amplitude (the size of the oscillation) will follow SHM. SHM is a consequence of Hooke’s Law, which describes a restoring force F, which is linearly proportional to the displacement from equilibrium:

(The minus sign is the “restoring” part.) Hooke’s Law can also be represented graphically, by a line with a slope of -k:

The basic system for understanding Hooke’s Law and SHM is a mass attached to a spring. If the mass is m and the spring constant or “springiness” of the spring is k (in Newtons/meter), then the period of oscillation T is given by

.

That is to say, smaller masses will produce shorter periods of oscillation, as will stiffer springs. Note that in the above formula, the period of oscillation does not depend on the amplitude, but it does depend on the mass.

Now let us turn our attention to Portal. If you drop from rest at a height h, the time it takes to reach the ground is found (using ) to be

.

The time it takes to fall from height h and go through, say, a blue portal in the floor, come out the orange portal in the floor and reach a height h again is thus 2 t_Fall. But this is only half an oscillation cycle. The full cycle is when you fall back through the orange portal, come out the blue side, and reach height h. Thus, the period of oscillation for jumping-through-portal oscillations is

.

Now h is the size of the oscillation, i.e. it is the amplitude. We see here that the period of these oscillations does depend on the amplitude – jumping off a higher point will produce a longer period of oscillation. Furthermore we see that the mass of whatever is oscillating (e.g., your body) is not a factor in the oscillation, and does not affect the period. This is because, instead of Hooke’s Law, the force of gravity on your body is constant with respect to displacement, and scales with the mass:

.

Another way of saying this is that all objects accelerate at the same rate in a constant gravitational field, and this is quite different from Hooke’s Law. (Hooke’s Law would be like the acceleration your body experiences being greater the higher up you are.)

Exercise 1: Show that , where h_ft is the initial height measured in feet.

Exercise 2: Go ahead and estimate the height from which you are about to drop into a portal, and use that to find the time it will take to reach the floor. Then multiply that by 4 and see if the time you get is the same as the time you measure by playing the game with a stopwatch in hand!

College Physics:

Visually, oscillations in and out of the floor in Portal look very much like SHM. The oscillating object (or body) has a maximum speed at the floor, and gradually slows as it reaches a maximum.

To show how similar this motion is to SHM, let’s plot a graph. If we graph the height of the object/body as a function of time, we get a waveform. To help in the comparison with SHM, we’ll assume you drop into a blue portal, and regard any heights reached on the “orange portal side” as negative heights. If we do this, the comparison with SHM is striking:

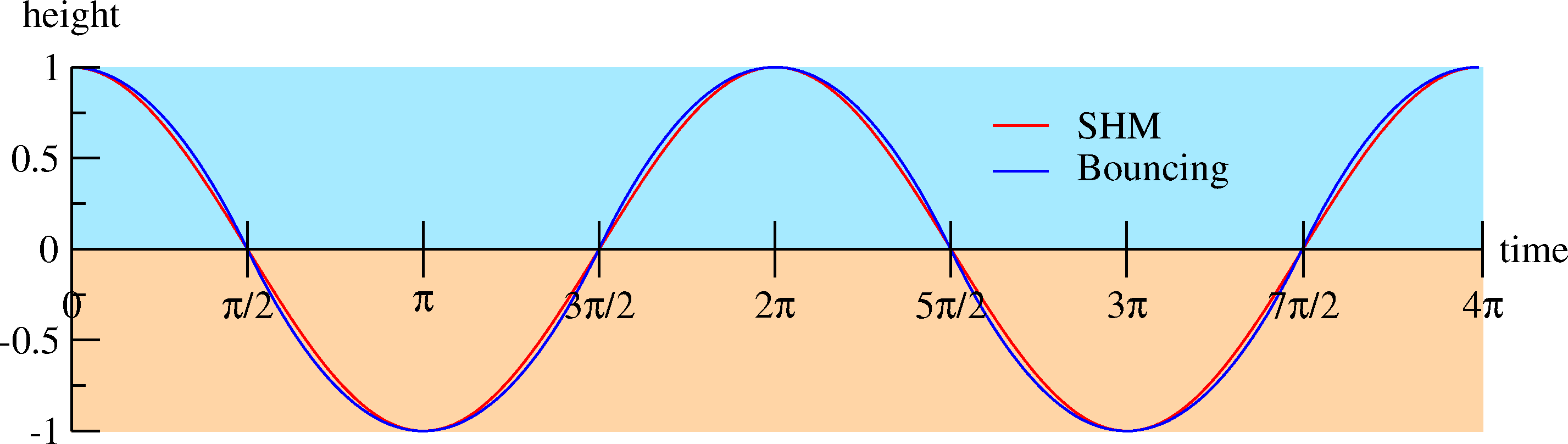
The red line is sinusoidal and shows displacement vs. time for simple harmonic motion. The blue line is a graph of oscillatory motion in and out of two portals on the floor in a uniform gravitational field. (The amplitudes and periods have been normalized for the purposes of comparison.) Note how close these curves are! No wonder the oscillation in and out of portals looks like SHM!

There’s more to these curves than meets the eye. The red curve is sinusoidal, whereas the blue curve is piecewise parabolic. Both are continuous functions, and have continuous first derivatives.

Let’s compare the first derivatives, i.e. the velocities of the motion:

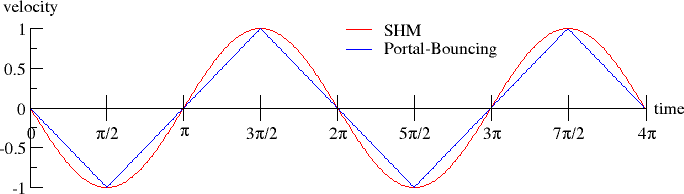
See how the red line switches phase by 90 degrees, whereas the blue line becomes a triangle wave? Let’s take another derivative and look at the accelerations:

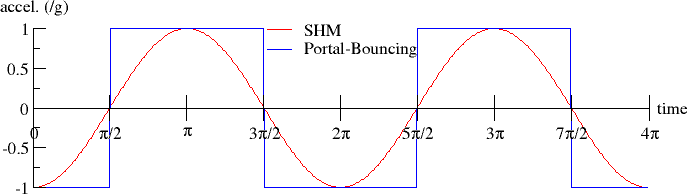
Now we can see the crux of the differences in the motion. The red curve is still sinusoidal and continuous but the blue one has become a square wave, which is discontinuous. This is due to the discontinuity in the gravitational field that occurs as you go through the floor: it instantly switches from pulling in one direction to pulling in the other. And, as we said earlier, the force (/acceleration) doesn’t depend on the displacement from equilibrium, so larger amplitudes don’t result in larger accelerations, they simply result in longer oscillation periods.

Exercise: Instead of a creating a portal, imagine you can create a hole that goes all the way through the earth. You jump from the earth’s surface into the hole and come out the other side.. Regarding the earth as a sphere of uniform density, show that the resulting motion is simple harmonic, with a period of about 80 minutes.

Afterward: What it “Feels” Like

So far we have neglected a fine point: We have been regarding the body in motion as a single particle of zero extent, centered at the person’s “center of mass.” This is likely how the game developers employed the physics engine when writing the game. The trouble is that the concept of “center of mass” becomes meaningless when the body is disjoint and subject to discontinuous gravitational fields. When you are “in” the portal, such that parts of your body (from your waist down, say) are sticking out of the orange portal, while the rest of you is sticking out of the blue portal, you have no single center of mass, you have two: one for each piece of your body which is outside a portal.

Furthermore, these two masses are both being attracted back inside the portal. Your upper body is getting pulled into with a force equal to its weight --- in the direction of your feet --- while the lower half of your body is getting pulled back into the portal with a force equal to its weight, in the direction of your head.

This is the kind of thing you experience all the time, just standing on a floor. Your body gets pulled down by its weight, and the floor pushes back back up with exactly the same amount of force, so your net acceleration is zero. What you feel is the floor pushing up on you, and/or your legs pushing down onto the floor.

The same thing happens as you are going through a portal…sort of. In this case, it is the weight of however much of your lower body is sticking out of the portal – not your entire weight -- which pushes on your upper body.

You feel this precisely at the spot where your body is in the plane of the floor, i.e. wherever the portal “cuts” your body. Thus, as you start to go into the portal, you feel a slight pushing at the bottom of your feet. This sensation rises along your legs, getting stronger (in a more or less linear fashion) as the plane of intersection progresses up your body as it moves through the portal. The force reaches a maximum when you are halfway through, and the sensation continues traveling up toward you head, getting weaker and weaker until your head is finally through, and you travel upwards (feet first), completely out of the orange portal.

Note that when you are exactly half-way through the portal, such that half your weight is pushing in one direction (relative to you) and the other half is pushing in the other, the net force on you is zero.

With these observations in mind, the acceleration graph becomes no longer a square wave. Instead, the vertical sides of each “square” are no longer vertical but instead “slanted”, resulting in what one might call a “trapezoid” wave.

Curious to experience the feeling of one “g” of acceleration occurring in a thin slice of your body, moving up and down as you go through each portal? Submit a feature request to Valve! ☐

---

Scott Hawley is a computational astrophysicist at Belmont University in Nashville, TN, where he advises the Society of Physics Students and teaches classes for audio engineers.